NEWS
Mathe-Genie gesucht (Kurvenberechnung)
-
@gargano sagte in Mathe-Genie gesucht (Kurvenberechnung):
Abfrage bringt ein Json mit den stündlichen Werten, sowie gesamt Wert
Danke, aber ich glaube wir reden aneinander vorbei.
ich brauche nicht den erwarteten Wert des Tages, sondern den an diesem Tag möglichen Maximalwert (grob gerechnet reicht) für diese StundeMit diesem möchte ich dann den Istwert vergleichen und abschätzen, ob es bewölkt, bedeckt oder sonnig ist
@homoran sagte in Mathe-Genie gesucht (Kurvenberechnung):
@gargano sagte in Mathe-Genie gesucht (Kurvenberechnung):
......Danke, aber ich glaube wir reden aneinander vorbei.
ich brauche nicht den erwarteten Wert des Tages, sondern den an diesem Tag möglichen Maximalwert (grob gerechnet reicht) für diese Stundeachso... hab es jetzt wohl erst verstanden. Ist also nicht abhängig vom Wetter sondern abhängig vom Sonnenstand?
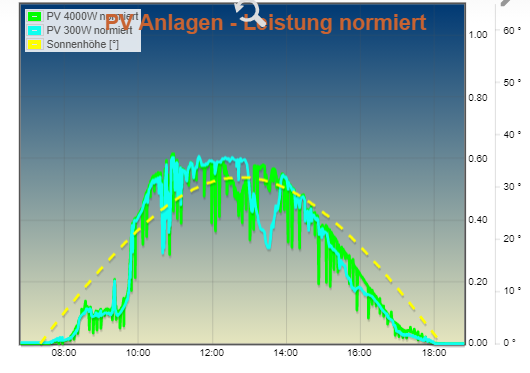
Ich lass bei mir die Sonnenhöhe mitlaufen. Ist das was? Hier am Beispiel von gestern:
-
@homoran sagte in Mathe-Genie gesucht (Kurvenberechnung):
@gargano sagte in Mathe-Genie gesucht (Kurvenberechnung):
......Danke, aber ich glaube wir reden aneinander vorbei.
ich brauche nicht den erwarteten Wert des Tages, sondern den an diesem Tag möglichen Maximalwert (grob gerechnet reicht) für diese Stundeachso... hab es jetzt wohl erst verstanden. Ist also nicht abhängig vom Wetter sondern abhängig vom Sonnenstand?
Ich lass bei mir die Sonnenhöhe mitlaufen. Ist das was? Hier am Beispiel von gestern:

-
@homoran sagte in Mathe-Genie gesucht (Kurvenberechnung):
@gargano sagte in Mathe-Genie gesucht (Kurvenberechnung):
......Danke, aber ich glaube wir reden aneinander vorbei.
ich brauche nicht den erwarteten Wert des Tages, sondern den an diesem Tag möglichen Maximalwert (grob gerechnet reicht) für diese Stundeachso... hab es jetzt wohl erst verstanden. Ist also nicht abhängig vom Wetter sondern abhängig vom Sonnenstand?
Ich lass bei mir die Sonnenhöhe mitlaufen. Ist das was? Hier am Beispiel von gestern:

@lobomau sagte in Mathe-Genie gesucht (Kurvenberechnung):
Ist das was?
leider nein.
Das ist ja was @Gargano schreibt. Bei einer Ausrichtung auf 180° geht das noch einigermaßen -
@gargano sagte in Mathe-Genie gesucht (Kurvenberechnung):
Kannst Du Beispieldaten für einen Tag posten
muss ich mal sehen wie ich den aus History rausbekomme.
Der Download der Daten in den Objekts funktioniert ja (zumindest bei mir) immer noch nicht@gargano sagte in Mathe-Genie gesucht (Kurvenberechnung):
Wird aber etwas dauern, so aus dem Ärmel kann ich das auch nicht schütteln.
Um Himmels Willen!
Danke, dass du hilfst! Nimm dir alle Zeit dafür -
@homoran
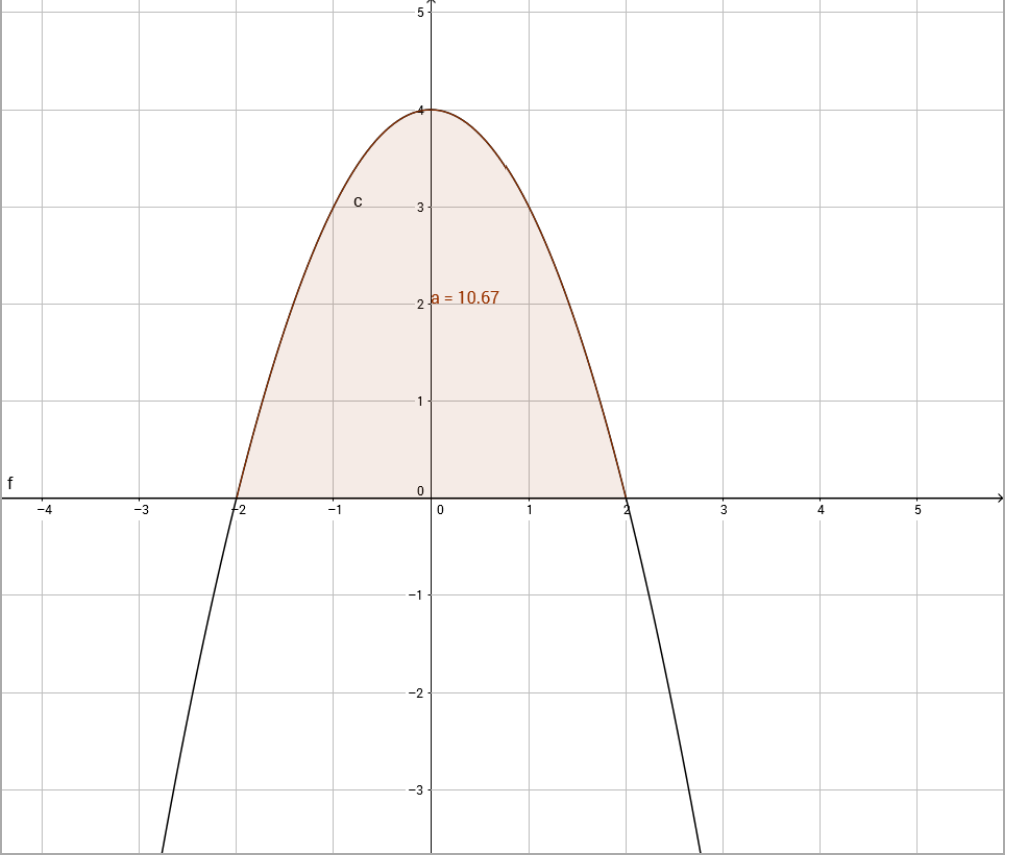
Wenn du davon ausgehen kannst, dass die Parabel symmetrisch ist, dann kannst du das nach folgender Formel berechnen:Hier in dem Beispiel sind x=-2 und x=2 die Nullstellen.
f(x) = -(x-2)(x+2)
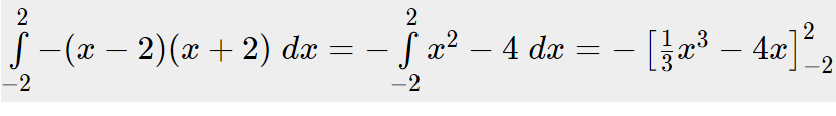
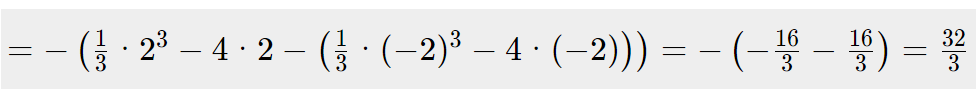
Hier zur Verdeutlichung die Parabel:
@martybr sagte in Mathe-Genie gesucht (Kurvenberechnung):
Wenn du davon ausgehen kannst, dass die Parabel symmetrisch ist
kann ich nicht - wird aber als solche definiert ;-)
@martybr sagte in Mathe-Genie gesucht (Kurvenberechnung):
dann kannst du das nach folgender Formel berechnen:
ich wohl eher nicht.
Muss mal sehen, wie ich das umsetzeDas ist anscheinend genau das, was ich suche
-
@martybr sagte in Mathe-Genie gesucht (Kurvenberechnung):
Wenn du davon ausgehen kannst, dass die Parabel symmetrisch ist
kann ich nicht - wird aber als solche definiert ;-)
@martybr sagte in Mathe-Genie gesucht (Kurvenberechnung):
dann kannst du das nach folgender Formel berechnen:
ich wohl eher nicht.
Muss mal sehen, wie ich das umsetzeDas ist anscheinend genau das, was ich suche
@homoran Du kannst es ja vereinfachen. Setze das Integral doch von "0" bis zum 2. Schnittpunkt und verdopple den Wert. Der zweite Schnittpunkt entspricht somit der Breite der Parabel.
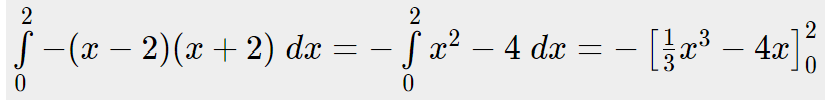
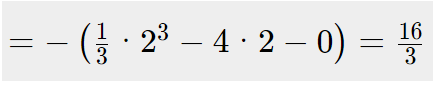
Das Ergebnis mal 2 nehmen. Die Formel ist einfacher umzusetzen.
-
@homoran Du kannst es ja vereinfachen. Setze das Integral doch von "0" bis zum 2. Schnittpunkt und verdopple den Wert. Der zweite Schnittpunkt entspricht somit der Breite der Parabel.
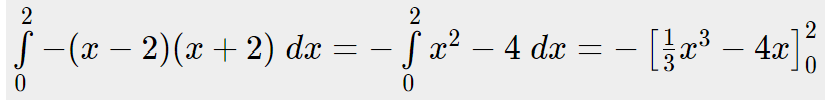
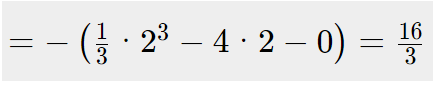
Das Ergebnis mal 2 nehmen. Die Formel ist einfacher umzusetzen.
@martybr sagte in Mathe-Genie gesucht (Kurvenberechnung):
Setze das Integral doch von "0" bis zum 2. Schnittpunkt und verdopple den Wert
die Schnittpunkte sind im Prinzip die Zeiten für Elevation >0 und somit leicht zu ermitteln, wobei im Sommer noch etwas Sonne von "Hinten" auf die Panels fallen würde, was zu vernachlässigen ist.
Wenn du mit "0" den Apex meinst, also der Sonnenmittag ist der Ansatz mit Sonnenaufgang - Sonnenmittag x 2 sicher die sinnvollste.
@martybr sagte in Mathe-Genie gesucht (Kurvenberechnung):
Du kannst es ja vereinfachen
Aber wie gebe ich ein Integral in (Blockly) js ein?
-
@martybr sagte in Mathe-Genie gesucht (Kurvenberechnung):
Setze das Integral doch von "0" bis zum 2. Schnittpunkt und verdopple den Wert
die Schnittpunkte sind im Prinzip die Zeiten für Elevation >0 und somit leicht zu ermitteln, wobei im Sommer noch etwas Sonne von "Hinten" auf die Panels fallen würde, was zu vernachlässigen ist.
Wenn du mit "0" den Apex meinst, also der Sonnenmittag ist der Ansatz mit Sonnenaufgang - Sonnenmittag x 2 sicher die sinnvollste.
@martybr sagte in Mathe-Genie gesucht (Kurvenberechnung):
Du kannst es ja vereinfachen
Aber wie gebe ich ein Integral in (Blockly) js ein?
-
@martybr sagte in Mathe-Genie gesucht (Kurvenberechnung):
Setze das Integral doch von "0" bis zum 2. Schnittpunkt und verdopple den Wert
die Schnittpunkte sind im Prinzip die Zeiten für Elevation >0 und somit leicht zu ermitteln, wobei im Sommer noch etwas Sonne von "Hinten" auf die Panels fallen würde, was zu vernachlässigen ist.
Wenn du mit "0" den Apex meinst, also der Sonnenmittag ist der Ansatz mit Sonnenaufgang - Sonnenmittag x 2 sicher die sinnvollste.
@martybr sagte in Mathe-Genie gesucht (Kurvenberechnung):
Du kannst es ja vereinfachen
Aber wie gebe ich ein Integral in (Blockly) js ein?
@homoran Ganz so einfach ist es nicht, da die Funktion f(x) = -(x-2)(x+2) nur ein Beispiel war.
Allgemein ist es f(x) = -(ax-b)(ax+b), wobei weder a noch b bekannt sind . Die gilt es aus den gegebenen Anfangswerten zu ermitteln. Die werden sich dann mit Laufe des Sonnenstandes und Daten stark verändern. -
@homoran Ganz so einfach ist es nicht, da die Funktion f(x) = -(x-2)(x+2) nur ein Beispiel war.
Allgemein ist es f(x) = -(ax-b)(ax+b), wobei weder a noch b bekannt sind . Die gilt es aus den gegebenen Anfangswerten zu ermitteln. Die werden sich dann mit Laufe des Sonnenstandes und Daten stark verändern.@gargano wie gesagt kommt es mir nicht auf 100%ige Korrektheit an.
Eine annähernde Form (die auch noch einfach symmetrisch, da der Anstieg der wichtigere Teil ist) reicht mir vollkommen.Mit der Extraktion der Daten hänge ich leider immer noch fest.
@gargano sagte in Mathe-Genie gesucht (Kurvenberechnung):
wobei weder a noch b bekannt sind . Die gilt es aus den gegebenen Anfangswerten zu ermitteln
das sollte IMHO zu schaffen sein.
Ich denke, dass eine Veränderung im Lauf vernachlässigt werden kann -
@gargano wie gesagt kommt es mir nicht auf 100%ige Korrektheit an.
Eine annähernde Form (die auch noch einfach symmetrisch, da der Anstieg der wichtigere Teil ist) reicht mir vollkommen.Mit der Extraktion der Daten hänge ich leider immer noch fest.
@gargano sagte in Mathe-Genie gesucht (Kurvenberechnung):
wobei weder a noch b bekannt sind . Die gilt es aus den gegebenen Anfangswerten zu ermitteln
das sollte IMHO zu schaffen sein.
Ich denke, dass eine Veränderung im Lauf vernachlässigt werden kann -
Gibt es eine Möglichkeit eine annähernde Berechnunug der zu erwartenden maximalen Solarleistung anhand der Kurven in eine Formel zu gießen?
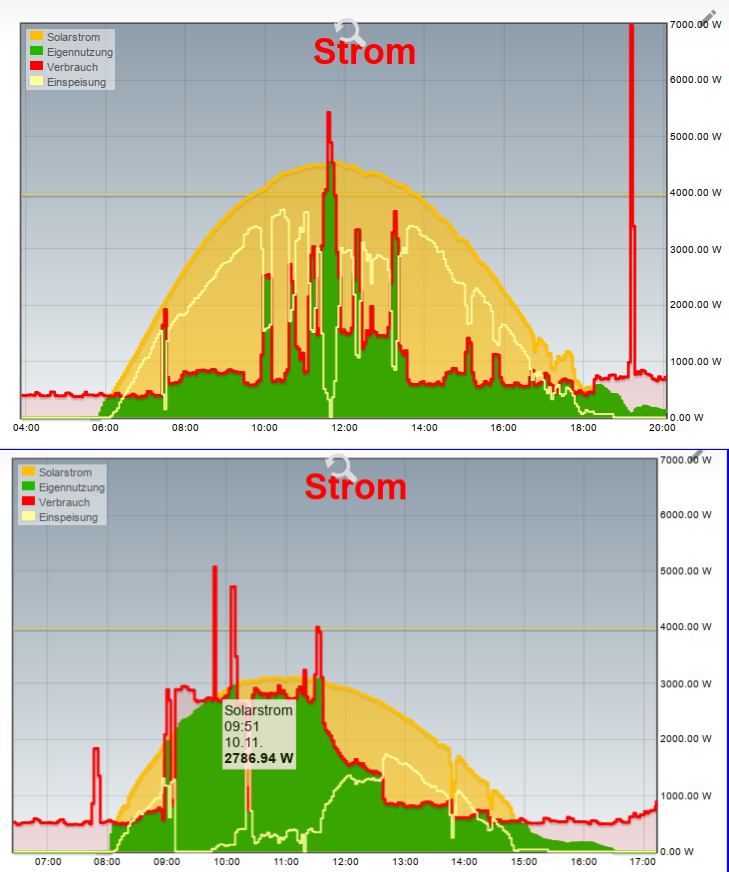
Hier sind Kurven meines Solaretrags, jeweils möglichst optimal annähernd zur Sommer- und zur Wintersonnenwende.
Ich würde gerne irgendwie anhand von Uhrzeit (besser wohl Azimut) bei Sonnenaufgang und maximale Elevation zum Sonnenmittag berechnen wie hoch zu einer bestimmten Zeit in der Kurve die Produktion im Optimalfall annähernd sein könnte, um den "Bedeckungsgrad" abschätzen zu können
@homoran sagte: annähernde Berechnunug der zu erwartenden maximalen Solarleistung
Die Leistung abhängig von der Uhrzeit bei klarem Himmel?
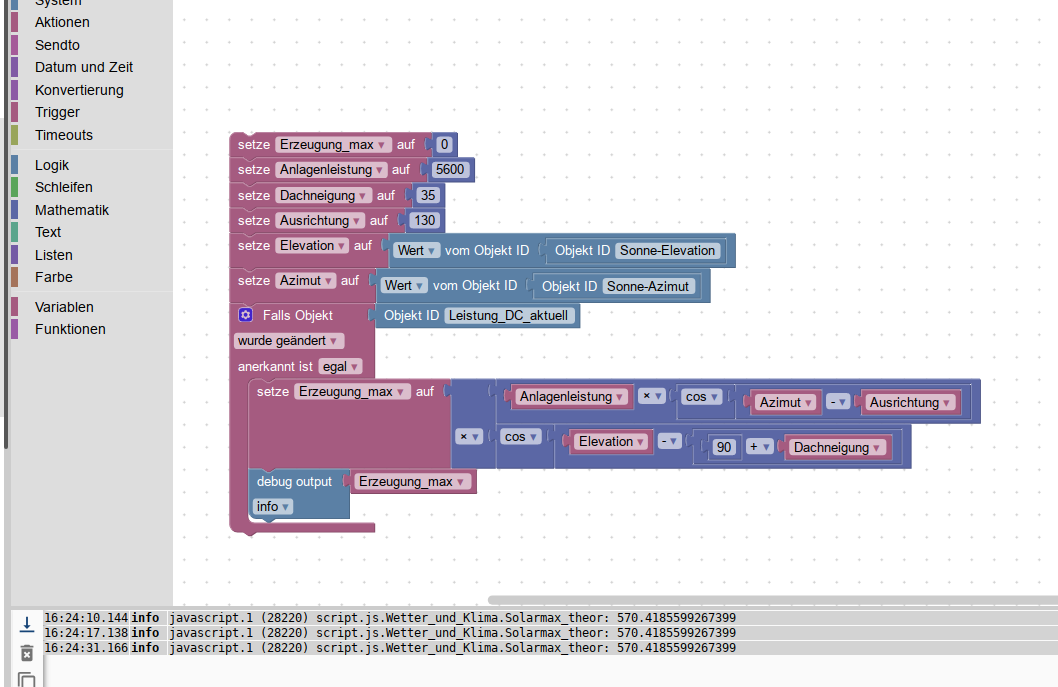
Für die direkte Sonneneinstrahlung (ohne diffuse Strahlung) sollte folgender Zusammenhang gelten:
p = ps * cos(Azimut - Ausrichtung) * cos(Elevation - (90° - Neigung))- ps = Leistung, wenn die Sonnenstrahlung senkrecht auf das Modul einfällt
- Neigung = Modulneigung, waagerecht = 0
Diese Formel berücksichtigt nicht den längeren Weg der Strahlung durch die Atmosphäre bei niedrigem Sonnenstand.
-
@homoran sagte: annähernde Berechnunug der zu erwartenden maximalen Solarleistung
Die Leistung abhängig von der Uhrzeit bei klarem Himmel?
Für die direkte Sonneneinstrahlung (ohne diffuse Strahlung) sollte folgender Zusammenhang gelten:
p = ps * cos(Azimut - Ausrichtung) * cos(Elevation - (90° - Neigung))- ps = Leistung, wenn die Sonnenstrahlung senkrecht auf das Modul einfällt
- Neigung = Modulneigung, waagerecht = 0
Diese Formel berücksichtigt nicht den längeren Weg der Strahlung durch die Atmosphäre bei niedrigem Sonnenstand.
@paul53 sagte in Mathe-Genie gesucht (Kurvenberechnung):
Die Leistung abhängig von der Uhrzeit bei klarem Himmel?
Ja! die mögliche Leistung....
@paul53 sagte in Mathe-Genie gesucht (Kurvenberechnung):
Diese Formel berücksichtigt nicht den längeren Weg der Strahlung durch die Atmosphäre bei niedrigem Sonnenstand.
Das sind unnötige Feinheiten.
@paul53 sagte in Mathe-Genie gesucht (Kurvenberechnung):
p = ps * cos(Azimut - Ausrichtung) * cos(Elevation - (90° - Neigung))
das klingt wieder viel zu einfach ;-)
ist ja die theoretische Bestrahlung.Da muss dann noch irgendwo der Modulwirkungsgrad rein, oder?
-
@paul53 sagte in Mathe-Genie gesucht (Kurvenberechnung):
Die Leistung abhängig von der Uhrzeit bei klarem Himmel?
Ja! die mögliche Leistung....
@paul53 sagte in Mathe-Genie gesucht (Kurvenberechnung):
Diese Formel berücksichtigt nicht den längeren Weg der Strahlung durch die Atmosphäre bei niedrigem Sonnenstand.
Das sind unnötige Feinheiten.
@paul53 sagte in Mathe-Genie gesucht (Kurvenberechnung):
p = ps * cos(Azimut - Ausrichtung) * cos(Elevation - (90° - Neigung))
das klingt wieder viel zu einfach ;-)
ist ja die theoretische Bestrahlung.Da muss dann noch irgendwo der Modulwirkungsgrad rein, oder?
@homoran sagte: Da muss dann noch irgendwo der Modulwirkungsgrad rein, oder?
@paul53 sagte in Mathe-Genie gesucht (Kurvenberechnung):
Leistung, wenn die Sonnenstrahlung senkrecht auf das Modul einfällt
Meint die Modulleistung, nicht die Strahlungsleistung der Sonne.
-
@homoran sagte: Da muss dann noch irgendwo der Modulwirkungsgrad rein, oder?
@paul53 sagte in Mathe-Genie gesucht (Kurvenberechnung):
Leistung, wenn die Sonnenstrahlung senkrecht auf das Modul einfällt
Meint die Modulleistung, nicht die Strahlungsleistung der Sonne.
Meint die Modulleistung, nicht die Strahlungsleistung der Sonne.
Danke - hatte ich nicht als solche gelesen, also (k)Wp des Systems
-
@paul53 sagte in Mathe-Genie gesucht (Kurvenberechnung):
Die Leistung abhängig von der Uhrzeit bei klarem Himmel?
Ja! die mögliche Leistung....
@paul53 sagte in Mathe-Genie gesucht (Kurvenberechnung):
Diese Formel berücksichtigt nicht den längeren Weg der Strahlung durch die Atmosphäre bei niedrigem Sonnenstand.
Das sind unnötige Feinheiten.
@paul53 sagte in Mathe-Genie gesucht (Kurvenberechnung):
p = ps * cos(Azimut - Ausrichtung) * cos(Elevation - (90° - Neigung))
das klingt wieder viel zu einfach ;-)
ist ja die theoretische Bestrahlung.Da muss dann noch irgendwo der Modulwirkungsgrad rein, oder?
@homoran Wobei jetzt die Richtung in theoretische Einstrahlung geht, etwas anderes als oben von Dir angedacht.
Ich habe von meiner früheren Arbeit den Code für quadratische Regression wiedergefunden, eigentlich daß was Du am Anfang angefragt hattest. -
@homoran Wobei jetzt die Richtung in theoretische Einstrahlung geht, etwas anderes als oben von Dir angedacht.
Ich habe von meiner früheren Arbeit den Code für quadratische Regression wiedergefunden, eigentlich daß was Du am Anfang angefragt hattest.@gargano
Sei mir nicht böse, ich hatte es so gedacht, wie du es verstanden hattest (PS hab jetzt die History-Daten als JSON mit 50k Zeilen ;-) - nutzt dir das was?)Werde es aber erst mal nach Pauls Ansatz machen, weil den sogar ich verstehe
Ist mal wieder ein typischer Paul: anderer Ansatz - viel einfacher. Und wahrscheinlich durchaus für meine Zwecke ausreichend.Danke euch erst einmal - bin schon am basteln ;-)
muss jetzt nur noch die Sonnenstandswerte in Blockly finden. Sollen ja damit ohne separates Programm gehen. -
-
@homoran sagte: läuft soweit
Falscher Operator vor Dachneigung: + --> -
@homoran sagte in Mathe-Genie gesucht (Kurvenberechnung):
wie oft die aktualisiert wird.
Nimm einen Zeitplan (jede Minute) und setze die Variablen Azimut und Elevation innerhalb des Triggers.